mbrt: Sphere Class Reference

Sphere::Sphere	(	Point3D	center,
		double	r
	)			`[inline]`

Create a sphere.

Definition at line 44 of file sphere.h.

References log_debug, Renderable::m_center, Point3D::x, Point3D::y, and Point3D::z.

Sphere::~Sphere ( ) [virtual]

Clean up the sphere's resources.

Definition at line 16 of file sphere.cpp.

bool Sphere::collides_with	(	const Ray &	ray,
		double &	t
	)			const `[virtual]`

Determine if a ray intersects this object.

Any point along a ray:

$p = u + dt$

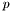Where $p$ is the point along the ray, 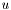$u$ is the ray's origin, 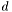$d$ is the ray's direction and 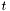$t$ is how far down the ray the point is.

The equation of a sphere is:

$|I - C|^2 = r^2$

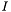Where $I$ is any point on the sphere's surface, 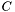$C$ is the sphere's m_center, and 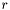$r$ is the sphere's radius.

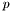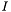We need to find all points where the ray intersects the sphere. That is we need to find all places where the ray is on the surface of the sphere, so we substitute $p$ for $I$ , yielding:

$|(u + dt) - C|^2 = r^2$

We can safely drop the absolute value, since it will be squared anyway. Simplifying, we arrive at:

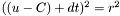
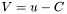Where , yields: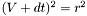

Further simplifying:

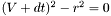
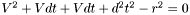
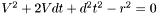
Arranging in a form more suitable for the quadratic equation:

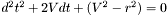
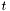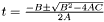Solving for $t$ using the quadratic equation $t = \frac{-B \pm \sqrt{ B^2 - 4AC}}{2A}$ :

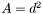
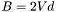
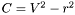
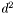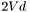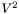It should be noted $d^2$ , $2Vd$ , and $V^2$ are all dot products, which yield a single scalar value. Accordingly:

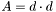
$A = d \cdot d$
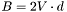
$B = 2V \cdot d$
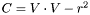
$C = V \cdot V - r^2$

Finally, The equation for $t$ is:

$t = \frac{-(2(V \cdot d)) \pm \sqrt{ (2(V \cdot d))^2 - 4(d \cdot d)(V \cdot V - r^2) }}{2(d \cdot d)}$

Which can be further simplified to:

$t = \frac{-((V \cdot d)) \pm \sqrt{ ((V \cdot d))^2 - (d \cdot d)(V \cdot V - r^2) }}{(d \cdot d)}$

We want to keep performance high, so we can take some shortcuts. For example, we can disregard all non-real numbers. This means that we can stop processing the equation when 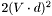$2(V \cdot d)^2$ is less than 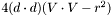$4(d \cdot d)(V \cdot V - r^2)$ , since the square root of a negative number is not a real number.

Parameters:

	ray	The ray we are testing to determine collision.
	t	The z-depth where the ray collides with this sphere.

Returns:: True if the ray collides with this sphere.

Implements Renderable.

Definition at line 20 of file sphere.cpp.

References Ray::direction(), dot_product(), Renderable::m_center, m_radius, and Ray::origin().

Here is the call graph for this function:

Ray Sphere::get_normal ( const Point3D & p ) const [virtual]

Return the surface normal of the sphere. A sphere's surface normal is the vector from the center of the sphere to the intersection point, translated to the intersection point and normalized.

Implements Renderable.

Definition at line 46 of file sphere.cpp.

References Renderable::m_center.

Sphere::StaticInit Sphere::m_init [static, protected]

Force static initialization.

Definition at line 36 of file sphere.h.

double Sphere::m_radius [protected]

The radius of the sphere.

Definition at line 39 of file sphere.h.

Referenced by collides_with().


Public Member Functions
virtual bool	collides_with (const Ray &ray, double &t) const
virtual Ray	get_normal (const Point3D &p) const
	Sphere (Point3D center, double r)
	Create a sphere.
virtual	~Sphere ()
	Clean up the sphere's resources.
Protected Attributes
double	m_radius
	The radius of the sphere.
Static Protected Attributes
static StaticInit	m_init
	Force static initialization.
Classes
class	StaticInit
	Fake a static initializer. More...

Sphere Class Reference

Public Member Functions

Protected Attributes

Static Protected Attributes

Classes

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation